Satellitengestützte Navigationssysteme

kannst Du in erster Näherung als ein Zwischending zwischen erdgebundenen elektronischen Navigationssystemen und der astronomischen Navigation betrachten.

Mit der erdgebundenen elektronischen Navigation haben diese 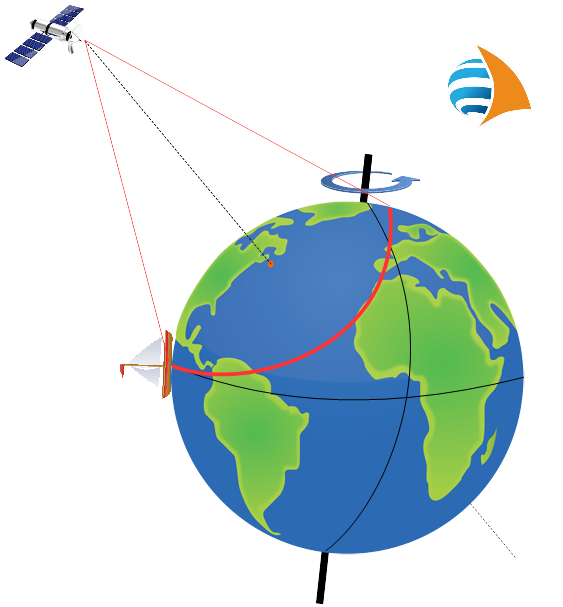Systeme gemeinsam, dass die Trilateration, also die Messung der Entfernungen zu mindestens 3 Satelliten der Berechnung von Standlinien (oder besser Standflächen) zugrunde gelegt wird. Im Gegensatz zur erdgebundenen elektronischen und in Gemeinsamkeit mit der astronomischen Navigation können die Standflächen aber für jeden einzelnen Satelliten getrennt berechnet werden. Es wird also nicht die Entfernungsdifferenz zu zwei Satelliten, sondern die tatsächliche Entfernung zu einem Satelliten zugrunde gelegt.

In die Navigation werden nur die Satelliten einbezogen, zu denen Sichtverbindung besteht. Man könnte sie also als Himmelskörper betrachten, Höhe und Azimut bestimmen und genauso verfahren, wie bei der astronomischen Navigation. Die Schwierigkeit wäre allerdings, dass sie noch näher als der Mond um die Erde kreisen, die Horizontalparallaxe also sehr großen Einfluss nehmen würde, und dass sie sich sehr schnell um die Erde bewegen. Außerdem sind sie im nautischen Jahrbuch nicht erfasst. Doch dazu später.

Alle Punkte, die die selbe Entfernung zu einem Satelliten haben, liegen auf der Oberfläche einer Kugel. Auch die Erde ist beinahe eine Kugel. Die beiden Kugeln schneiden sich in einem Kreis. Wie bei der astronomischen Navigation könnten wir so eine Standlinie erhalten.

Da die satellitengestützte Navigation aber nicht nur für die Seefahrt, sondern auch für die Luft- und Raumfahrt genutzt wird, müssen nicht nur Standorte auf der Erdoberfläche, sondern auch in der Luft und ganz allgemein im Raum ermittelt werden. Für die Luftfahrt würde es reichen, zusätzlich die Höhe über der Erdoberfläche zu berechnen, bei der Raumfahrt ist selbst das nicht ausreichend. Ganz so einfach, wie gerade eben geschildert, ist die Ortsbestimmung per Satellit also nicht.

Du fragst Dich gerade sicherlich, wie groß diese Kugeln sind. Das hängt natürlich davon ab, wo Du Dich befindest, auf einem Schiff, in einem Flugzeug oder einem Raumschiff, denn die Kugel gehen ja durch Deinen Standort hindurch. Vom Schiff aus betrachtet, entspricht der Radius der Kugeln maximal der Flughöhe des Satelliten plus dem Erddurchmesser (12.742 km). Die Satelliten der verschiedenen Navigationssysteme fliegen jeweils alle auf annähernd derselben Höhe.

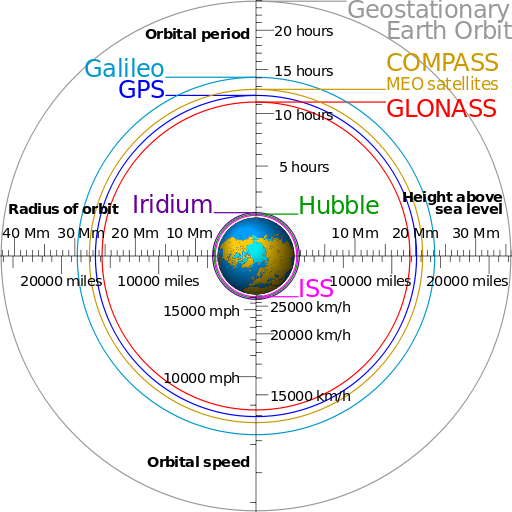Laufbahnen der Navigationssatelliten. Quelle. Wikipedia, Autor: cmglee
  1. bei GALLILEO fliegen die Satelliten auf 23.260 km Höhe mit einer Geschwindigkeit von 3,6 km/s
  2. GLONASS Satelliten sind mit etwa 3,9 km/s etwas schneller und fliegen auf 19.100 km Höhe
  3. GPS Satelliten, die auf 20.200 km Höhe fliegen, umkreisen die Erde mit 3,9 km/s
  4. BEIDOU (COMPASS) besteht auf 4 geostationären Satelliten auf 35.786 km Höhe über dem Äquator und zwölf Satelliten, die die Erde in einer Höhe von 22.000 km umkreisen.

 

< Zurück

Kurz und Knapp:

Bei der Satelliten-gestützten elektronischen Navigation werden die Entfernungen zu den Satelliten gemessen.

  1. Es wird keine Entfernungsdifferenz zwischen zwei, sondern die tatsächliche Entfernung zu einem bestimmten Satelliten gemessen.
  2. Bei bekannter Entfernung liegt der eigene Standpunkt auf der Oberfläche einer Kugel, in deren Mittelpunkt der Satellit steht.

Diese Kugel könnte mit der Erde (ideal auch eine Kugel) geschnitten werden, um eine Standlinie auf der Erdoberfläche zu erhalten. Das wird aber nicht gemacht, weil die Satelliten-gestützte Navigation auch für

  1. die Luftfahrt - hier wird zusätzlich die Höhe über dem Erdboden benötigt
  2. die Raumfahrt - benötigt einen allgemeinen Punkt im Raum.

genutzt wird.

Haben wir etwas unverständlich dargestellt? Magst Du selber einen Beitrag zu diesem Thema verfassen? Wenn ja, dann melde Dich doch schnell bei uns unter presse@segeln.de!

Wir freuen uns auf Dich!

 

Der allgemeine Ansatz

führt dazu, dass ein Standort im Raum ermittelt wird. Der Standort der Erde (des Erdmittelpunktes) im Raum ist bekannt, der Erdradius auch. Damit kann – ganz speziell für die Seefahrt und auch im Navigationssystem Deines Autos - von dem allgemein gehaltenen 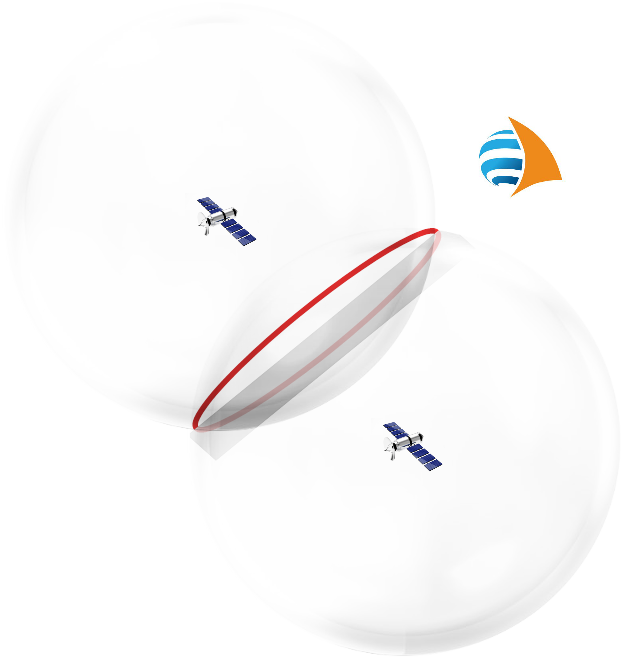Standort im Raum wieder auf einen Standort auf der Erdoberfläche zurückgerechnet werden.

Alle Punkte, die die selbe Entfernung zu einem Satelliten haben, liegen auf der Oberfläche einer Kugel, in deren Mittelpunkt der Satellit steht. Ist die Entfernung zu zwei Satelliten bekannt, ergeben sich zwei Kugeln, die sich in einem Kreis schneiden.

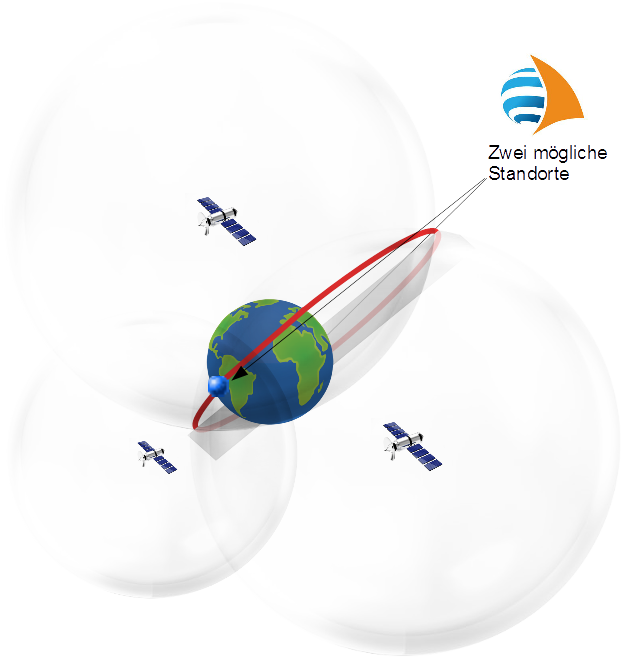Bei drei Satelliten sind es drei Kugeln. Je zwei davon schneiden sich in einem Kreis. Damit ergeben sich 3 Standlinien (Kreise), die sich in einem oder zwei Punkten schneiden. Du kannst es Dir auch so vorstellen, dass der Kreis, der sich aus dem Schnitt der ersten zwei Kugeln ergibt, an einem Punkt in die dritte Kugel eintritt und damit an einem anderen wieder austreten muss.

Einer dieser beiden Punkte ist der Standort des Empfängers. Der andere kann in der Regel durch Plausibilitätsüberlegungen ausgeschlossen werden - weil er bei der Seefahrtsanwendung zum Beispiel weit draußen im Weltraum liegen würde.

< Zurück

 

Ein Problem bleibt: Wie ermittelt der Empfänger die

Entfernung zum Satelliten

wenn Höhe und Azimut nicht herangezogen werden können?

Satelliten senden nicht nur ein Sinus-Signal, sondern nutzen ihre Trägerfrequenz um Nutzdaten zu transportieren. Diese Nutzdaten enthalten neben der Kennung des Satelliten seine aktuelle Position im Raum, den Stand seiner Uhr und Korrekturdaten für seine Zeit.

Damit der Satellit eine Uhrzeit mitliefern kann, hat er eine sehr genau gehende Atomuhr an Bord. Die Uhren aller Satelliten eines Navigationssystems sind synchronisiert. Da die gesendete Uhrzeit dem Stand der Uhr entspricht, zu dem ein Datenpaket den Satelliten verlassen hat, wird der Empfänger die Sendung zu einem späteren Zeitpunkt empfangen, denn das Datenpaket bewegt sich annähernd mit Lichtgeschwindigkeit und benötigt eine gewisse Zeit vom Satelliten zum Empfänger.

Wenn nun der Empfänger eine genauso gut synchronisierte Uhr wie der Satellit hätte, könnte er aus der Zeitdifferenz zwischen Empfang des Datenpakets und dem mitgelieferten Zeitstempel seine Entfernung zum Satelliten berechnen. Nun trägt aber nicht jeder eine synchronisierte Atomuhr in seiner Hosentasche spazieren – aber Du musst ja nicht alles selber haben, es reicht doch wenn Du jemanden fragen kannst, der eine Atomuhr hat, die mit dem des Satelliten synchron läuft: Du ziehst einfach mindestens einen weiteren Satelliten, der auch 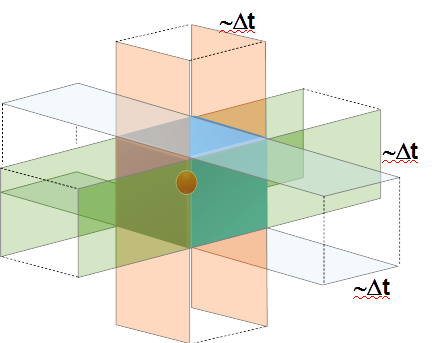die Uhrzeit sendet, als Referenz heran.

Bildlich kannst Du Dir das genauso vorstellen, wie das Fehlerdreieck bei der Kreuzpeilung. Würde die Uhr im Empfänger zu 100% mit denen der Satelliten synchron laufen, dann wäre die Kugelschale in der Skizze extrem dünn. Die drei Schalen treffen sich in einem Punkt. Da die Uhr aber ungenau geht, bekommen die Kugelschalen eine Dicke ~Δt. Die drei Schalen treffen sich nicht in einem Punkt, sondern in einem Quader, dessen Kantenlänge der Ungenauigkeit ~Δt der Uhr des Empfängers entspricht.

 

Um Dir ein Gefühl zu geben, wie dick diese Kugelschale denn nun wirklich ist:

Wenn Deine Uhr um 6ns (das sind 6 Tausendstel-Tausendstel-Tausendstel Sekunden) vor- oder nachgeht, dann ist die Schale der Kugel bereits 1m dick!

So wie beim Fehlerdreieck liegt Dein Standort wahrscheinlich nicht an einer der Ecken des Quaders (das wäre der vermeintliche Standort, den wir bis jetzt berechnet haben), sondern genau in der Mitte des Quaders.

Liegen nun die Daten eines vierten Satelliten vor, kann dessen Entfernung genauso berechnet werden, wie die der drei anderen. Sie kann aber auch als Entfernung zwischen dem gerade berechneten vermeintlichen Standort und der vom Satelliten übertragenen Satelliten-Position berechnet werden. Diese beiden Entfernungen werden aufgrund der Ungenauigkeit der Uhr in Deinem Empfänger nicht übereinstimmen. Aus der Differenz ergibt sich genau diese Ungenauigkeit ~Δt des Empfängers.

Das alles musst Du nicht selber rechnen. Dein GPS-, GLONASS-, GALLILEO- oder BEIDOU-Empfänger ist mit genügend Rechenleistung ausgestattet, um diese Fehlerkorrektur für Dich durchzuführen.

Er kann aber noch viel mehr mit den Daten anfangen, die die Satelliten ihm schicken. So kann er die Geschwindigkeit und Richtung ermitteln, mit der Du Deinen Empfänger bewegst. Er kann Routen berechnen und Tracks aufzeichnen, Dir mitteilen, wie sehr nach rechts oder links – backbord oder steuerbord – Du Dich drehen solltest, um Deinem Ziel näher zu kommen und Dir mitteilen, wann Du dieses wohl erreichen wirst.

Bleib bei uns, denn das alles und praktische Hinweise zu Deinem Satelliten-Empfänger findest Du in Kürze an dieser Stelle.

 

< Zurück

Das könnte Dich auch interessieren

Kurz und knapp:

  1. Alle Punkte, die sich im Raum gleich weit von einem Satelliten entfernt befinden, liegen auf einer Kugel, in deren Mittelpunkt der Satellit steht.
  2. Die Kugeln um zwei Satelliten schneiden sich in einem Kreis.
  3. Die Kugeln um drei Satelliten treffen sich in zwei Punkten.
  4. Einer der zwei Punkte ist der Standort des Satellitenempfängers, der andere fällt aufgrund von Plausibilitätsüberlegungen aus (z.B. weil er weit draußen im Weltraum liegt, während der Satelliten-Empfänger sich auf einem Schiff auf der Erdoberfläche befindet.)

Die Satelliten umkreisen die Erde in einer Flughöhe zwischen 19.100 km und 23.260 km. Das chinesische BEIDOU Navigationssystem setzt zusätzlich geostationäre Satelliten auf einer Flughöhe von 35.786 km ein.

 

Ungenauigkeit

Da die Uhr des Satelliten-Empfängers ungenau geht, nimmt die Dicke der Kugel-Schalen zu - je ungenauer die Uhr des Empfängers, desto dicker die Schale.

Die Schnitte der drei Kugeln ergeben daher einen Würfel, in dessen Mitte der Standort des Empfängers liegt.

Um die Ungenauigkeit der Uhr des Empfängers auszugleichen, werden die von einem vierten Satelliten übertragenen Daten herangezogen.

Geht die Uhr des Empfängers um 6ns (6 Tausendstel Tausendstel Tausendstel Sekunden) falsch, so beträgt die Ortsungenauigkeit bereits 1m.

 

Satelliten-Navigationssysteme benötigen daher zur Ortsbestimmung mindestens 4 Satelliten.